Cuando trabajamos con datos nos enfrentamos a diversos retos y en ocasiones no diferenciamos cuáles son más complejos. Por ejemplo, recolectar los datos puede ser difícil, pero extraer la información (a través de una óptima interpretación) tiene mayores complicaciones.
Un ejemplo de esto es que estamos acostumbrados a trabajar una estadística básica en torno a métricas que centralizan datos y no tanto con sus contrapartes. Aunque dicho de otro modo, más que medidas contrarias, las medidas de dispersión son la pieza faltante en el rompecabezas.
¿Quieres entender más sobre esto?
Veamos de qué se trata, cómo se calculan y un ejemplo práctico.
Qué son las medidas de dispersión
En estadística, las medidas de dispersión forman parte de un conjunto de datos específicos que revelan el comportamiento o la relación de las variables que se estudian. No obstante, esta relación se analiza desde un enfoque de “distanciamiento” o “separación”.
Cabe destacar que mientras algunas métricas de centralización, como la media, mediana o la moda, pretenden unificar los datos, cuando hablamos de dispersión se analiza la distancia entre los mismos datos. Por ejemplo: si calculando el Valor del Ticket promedio en dos días de facturación, y en uno hay $2M mientras que en el anterior hay $10M, habría una media de $6M ¿Correcto?
Ahora bien, ¿consideras correcto que para una proyección en ventas, se tome como referencia la media? Personalmente, no creo que sea suficiente; si durante una semana el valor del ticket está en $5M ¿Es favorable o no?
Por ello, y para una comprensión más profunda del caso, es necesario conocer otro tipo de detalles como lo son:
- Rango
- Desviación media
- Varianza
- Desviación típica o estándar
Rango
En primera instancia, tenemos esta medida que representa la distancia entre el valor máximo y el valor mínimo a estudiar. Su cálculo es simple y nos revela cuán amplio es el caso de estudio.
Solo debes tomar el valor máximo y restar el mínimo. Así tendrás una apreciación directa de la amplitud de los valores.

Desviación media
Esta medida de dispersión, propone relacionar los datos de la siguiente manera: Toma el valor absoluto de la resta de cada Variable y la Media, suma y divide entre N, o la cantidad de valores.

Varianza
Por su parte, s2 es igual a la sumatoria cuadrada de cada variable menos la media, que posteriormente se divide entre N, o la cantidad de valores.

Desviación típica o estándar
Finalmente, encontramos una medida de dispersión que deriva de la varianza, y es que a fin de simplificar, se considera la desviación típica para eliminar los cuadrados en el tratamiento de los datos. De hecho, esta medida es la raíz cuadrada de la varianza.
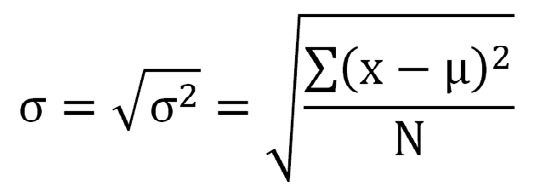
Nada complicado ¿O sí?
Medidas de dispersión para mayor comprensión del caso
Siguiendo con el ejemplo del ticket promedio, ya tenemos la media, pero a pesar de que esta es de $6M, estamos trabajando en un rango de $8M, lo cual hace que la probabilidad de estar fuera de la media, es bastante grande.
La desviación media se sitúa en los $4M, con una varianza de $0 y una desviación típica igual de nula.